Contenido

 Método Simplex:

       El Método Simplex es un método iterativo que permite ir mejorando la solución en cada paso. La razón matemática de esta mejora radica en que el método consiste en caminar del vértice de un poliedro a un vértice vecino de manera que aumente o disminuya (según el contexto de la función objetivo, sea maximizar o minimizar), dado que el número de vértices que presenta un poliedro solución es finito siempre se hallará solución. 

        Antes de empezar es necesario definir ciertos términos que son muy usados en los procedimientos del método:

Variables

Son aquellos datos que representan las incógnitas del problema

Restricciones

Se contemplan las limitaciones a las que se encuentra sujeta la resolución del problema considerando la escasez de recursos en tiempo y espacio. 

Función Objetivo

Representa la meta que se pretende alcanzar y en la cual se basan las decisiones principales para maximizar los beneficios o bien para minimizar los costos (considere que en la programación lineal el calificativo “lineal” hace referencia que las ecuaciones usadas en el modelo serán siempre de primer grado, es decir, sin exponentes).

A la hora de empezar a realizar el modelo de variables y funciones, es importante tener en cuenta que no siempre serán todos iguales, se necesita usar la lógica y considerar cual será la forma de facilitar el análisis de dicho modelo.

Datos que se pueden tomar a consideración a la hora de realizar el modelo son:

• Entre más sencillo sea el modelo, mejor será el resultado. Un modelo complejo no siempre será la mejor solución.
• El modelo debe ser validado antes de ser implementado para saber si representa la situación real y en caso de no ser así habrá que hacer los ajustes correspondientes.
• Si se hacen las cosas de manera apresurada, el modelo saldrá mal. Debe hacerse un minucioso análisis de la información recabada para identificar que en verdad será útil para el modelo.
• Los modelos son un herramienta más el tomador de decisiones tendrá siempre la última palabra. 

Tipo de optimización:

Como se ha comentado, el objetivo del método consistirá en optimizar el valor de la función objetivo. Sin embargo se presentan dos opciones: obtener el valor óptimo mayor (maximizar) u obtener el valor óptimo menor (minimizar).

Además existen diferencias en el algoritmo entre el objetivo de maximización y el de minimización en cuanto al criterio de condición de parada para finalizar las iteraciones y a las condiciones de entrada y salida de la base. Así:

• Objetivo de maximización
• Condición de parada: cuando en la fila Z no aparece ningún valor negativo.
• Condición de entrada a la base: el menor valor negativo en la fila Z (o el de mayor valor absoluto entre los negativos) indica la variable Pj que entra a la base.
• Condición de salida de la base: una vez obtenida la variable entrante, la variable que sale se determina mediante el menor cociente P0/Pj de los estrictamente positivos.

• Objetivo de minimización
• Condición de parada: cuando en la fila Z no aparece ningún valor positivo.
• Condición de entrada a la base: el mayor valor positivo en la fila Z indica la variable Pj que entra a la base.
• Condición de salida de la base: una vez obtenida la variable entrante, la variable que sale se determina mediante el menor cociente P0/Pj de los estrictamente negativos.

No obstante, es posible normalizar el objetivo del problema con el fin de aplicar siempre los mismos criterios en lo referente a la condición de parada del algoritmo y a las condiciones de entrada y salida de las variables de la base. De esta forma, si el objetivo es minimizar la solución, se puede cambiar el problema a otro equivalente de maximización simplemente multiplicando la función objetivo por "-1". Es decir, el problema de minimizar Z es equivalente al problema de maximizar (-1)·Z. Una vez obtenida la solución será necesario multiplicarla también por (-1).

• Ventajas: No hay que preocuparse por nuevos criterios de parada, condición de entrada y salida de la base ya que se mantienen.
• Inconvenientes: En el caso de que la función tenga todos los coeficientes de sus variables básicas positivos, y además las restricciones sean del tipo de desigualdad "≤", al hacer el cambio dichos coeficientes quedan negativos cumpliéndose la condición de parada en la primera iteración (en la fila del valor de la función objetivo todos los valores son positivos o cero). Obteniéndose en este caso por defecto un valor óptimo para la función igual a 0.
• Solución: Realmente no existe este problema dado que para que la solución sea superior a 0 es necesario que alguna restricción tenga impuesta la condición "≥" (y se trataría de un modelo para el método de las dos fases). En el caso planteado, la solución real debe ser cero.

Cambio de signo de los términos independientes:

También se ha dicho que los términos independientes (bi) de cada ecuación deben ser no negativos para poder emplear el método Simplex. A tal fin, si alguna de las restricciones presenta un término independiente menor que 0 habrá que multiplicar por "-1" ambos lados de la inecuación (teniendo en cuenta que esta operación también afecta al tipo de restricción).

• Ventajas: Con ésta simple modificación de signos en las restricciones correspondientes se posibilita la aplicación del método Simplex al problema modelado.
• Inconvenientes: Puede resultar que en las restricciones donde tengamos que modificar los signos de las constantes, los tipos de desigualdad fueran "≤" (quedando tras la operación del tipo "≥") siendo necesario desarrollar el método de las Dos Fases. Este inconveniente no es controlable, aunque podría ocurrir el caso contrario y resultar beneficioso si los términos independientes negativos se presentan en todas aquellas restricciones con desigualdad de tipo "≥". Si existe alguna restricción del tipo "=" no supondría ninguna ventaja ni desventaja puesto que siempre sería de necesaria aplicación el método de las dos fases.

Normalización de las restricciones:

Otra de las condiciones del modelo estándar del problema es que todas las restricciones sean ecuaciones de igualdad (también llamadas restricciones de igualdad), por lo que hay que convertir las restricciones de desigualdad o inecuaciones en dichas identidades matemáticas.

La condición de no negatividad de las variables (x1,..., xn ≥ 0) es la única excepción y se mantiene tal cual.

• Restricción de tipo "≤"

  Para normalizar una restricción con una desigualdad del tipo "≤", hay que añadir una nueva variable, llamada variable de holgura xs (con la condición de no negatividad: xs ≥ 0). Esta nueva variable aparece con coeficiente cero en la función objetivo, y sumando en la ecuación correspondiente (que ahora sí será una identidad matemática o ecuación de igualdad).

  a11·x1 + a12·x2 ≤ b1  a11·x1 + a12·x2 + 1·xs = b1
• Restricción de tipo "≥"

  En caso de una desigualdad del tipo "≥", también hay que añadir una nueva variable llamada variable de exceso xs (con la condición de no negatividad: xs ≥ 0). Esta nueva variable aparece con coeficiente cero en la función objetivo, y restando en la ecuación correspondiente.

  Surge ahora un problema con la condición de no negatividad con esta nueva variable del problema. Las inecuaciones que contengan una desigualdad de tipo "≥" quedarían:

  a11·x1 + a12·x2 ≥ b1  a11·x1 + a12·x2 - 1·xs = b1

  Al realizar la primera iteración con el método Simplex, las variables básicas no estarán en la base y tomarán valor cero. En este caso la nueva variable xs, tras hacer cero a x1 y x2, tomará el valor -b1 y no cumpliría la condición de no negatividad. Es necesario añadir otra nueva variable xr, llamada variable artificial, que también aparecerá con coeficiente cero en la función objetivo y sumando en la restricción correspondiente. Quedando entonces de la siguiente manera:

  a11·x1 + a12·x2 ≥ b1  a11·x1 + a12·x2 - 1·xs + 1·xr = b1
• Restricción de tipo "="

  Al contrario de lo que cabría pensar, para las restricciones de tipo "=" (aunque ya son identidades) también es necesario agregar variables artificiales xr. Como en el caso anterior, su coeficiente será cero en la función objetivo y aparecerá sumando en la restricción correspondiente.

  a11·x1 + a12·x2 = b1  a11·x1 + a12·x2 + 1·xr = b1

En el último caso se hace patente que las variables artificiales suponen una violación de las leyes del álgebra, por lo que será necesario asegurar que dichas variables artificiales tengan un valor 0 en la solución final. De esto se encarga el método de las dos fases y por ello siempre que aparezcan este tipo de variables habrá que realizarlo.

En la siguiente tabla se resume según la desigualdad el tipo de variable que aparece en la ecuación normalizada, así como su signo:

Tipo de desigualdad	Tipo de variable que aparece
≥	- exceso + artificial
=	+ artificial
≤	+ holgura

Desarrollando el método Simplex:

Una vez estandarizado el modelo puede ocurrir que sea necesario aplicar el método Simplex o el método de las dos fases. Véase en la figura la forma de actuación para llegar a la solución del problema modelado.

Identificando casos anómalos y soluciones:

1. Solución óptima: cuando se cumple la condición de parada y no hay variables artificiales en la base con valor positivo (los valores se indican en la columna P0), se ha conseguido la optimización. El valor Z0 actual es la solución óptima del problema, cumpliéndose para las variables que se encuentran en la base. Si se trata de un problema de minimización, el valor óptimo obtenido se multiplicará por "-1".
2. Infinitas soluciones: cumplida la condición de parada, si alguna variable de decisión no básica tiene un valor 0 en la fila Z, significa que existe otra solución que aporta el mismo valor óptimo para la función objetivo. Es este caso el problema admite infinitas soluciones, estando todas ellas comprendidas dentro del segmento (o porción del plano, región del espacio, etc. dependiendo del número de variables del problema) definido por A·X1 + B·X2 = Z0. Mediante una nueva iteración y haciendo que la variable de decisión que tiene el 0 en la fila Z entre en la base se obtendrá otra solución diferente para el mismo valor óptimo.
3. Solución ilimitada (no acotada): si toda la columna de la variable que entra a la base tiene todos sus elementos negativos o nulos se trata de problema no acotado, es decir, que tiene solución ilimitada. No hay valor óptimo concreto para la función objetivo sino que a medida que se aumenta el valor de las variables también se incrementa el valor Z sin violar ninguna restricción.
4. No existe solución: cuando ningún punto satisface todas las restricciones del problema se produce la infactibilidad no existiendo ninguna solución posible para él. En este caso, una vez terminadas todas las iteraciones del algoritmo, existen en la base variables artificiales cuyo valor es superior a cero.
5. Empate de variable entrante: cuando se produce un empate en la condición de decisión de la variable entrante se puede optar por cualquiera de ellas sin que esto afecte a la solución final. Por contra si influye en el número de iteraciones necesarias para obtener dicha solución. Se aconseja optar a favor de las variables básicas ya que ellas son las que formarán parte de la solución óptima.
6. Empate de variable saliente: se puede nuevamente optar por cualquiera de ellas. Sin embargo, a fin de no alargar el problema y evitar la entrada en un bucle infinito (caso degenerado), se discrimina a favor de las variables de decisión haciendo que permanezcan en la base. En el caso de estar en la primera fase del método de las Dos Fases, se optará por sacar de la base las variables artificiales.
7. Curiosidad en la Fase 1: al finalizar la fase 1, si el problema original tiene solución, todas las variables artificiales en la fila indicadora deben tener el valor "1".
8. ¿El elemento pivote puede ser nulo?: No, el elemento pivote siempre será estrictamente positivo ya que únicamente se realizan los cocientes entre valores no negativos y mayores que cero (ante un problema de maximización).

Matriz Identidad

       Una matriz puede definirse como una ordenación rectangular de elementos, (o listado finito de elementos), los cuales pueden ser números reales o complejos, dispuestos en forma de filas y de columnas.

     La matriz idéntica o identidad es una matriz cuadrada (que posee el mismo número tanto de columnas como de filas) de orden n que tiene todos los elementos diagonales iguales a uno (1) y todos los demás componentes iguales a cero (0), se denomina matriz idéntica o identidad de orden n, y se denota por:

La importancia de la teoría de matrices en el Método Simplex es fundamental, dado que el algoritmo se basa en dicha teoría para la resolución de sus problemas.

Propiedades:

    Cuando realizamos operaciones con la matriz unidad no debemos ponernos nerviosos. Debemos pensar en la matriz identidad como si fuera el número uno (1).

Número 1

• Cuando multiplicamos por uno (1) cualquier otro número nos queda el mismo número (neutralidad). Dada una constante z o escalar cualquiera:  

Efecto neutro de la multiplicación de una constante con el número uno (1).

• Si hacemos el inverso del número uno (1), obtendremos el mismo número uno (1) (inversible).

Efecto neutro de hacer el inverso del número uno (1).

• Cuando elevamos el número uno (1) h unidades, siempre nos quedará el número uno (1) (idempotencia).

Efecto neutro de elevar el número uno (1) a una constante h.

Matriz identidad

• Neutralidad. Cuando la matriz unidad participa en una multiplicación de matrices, se dice producto neutro. Dada una matriz Z cualquiera:

Efecto neutro de multiplicar la matriz identidad por una matriz cualquiera.

• Inversible. La matriz inversa de la matriz unidad es la matriz identidad: 

Efecto neutro de invertir la matriz identidad.

• Idempotencia. La matriz inversa elevada h unidades (número natural) sigue siendo la matriz unidad: 

Efecto neutro de elevar h unidades la matriz identidad.

Procedimiento para identificar una matriz identidad

1. La matriz tiene que ser una matriz cuadrada.
2. La matriz debe tener unos (1) en la diagonal principal y ceros (0) en las otras posiciones. 

Aplicaciones

La matriz identidad participa en tantas ocasiones como el número uno (1) participa en álgebra. Por ejemplo, cuando multiplicamos una matriz cualquiera con su matriz inversa, obtendremos la matriz unidad.  

Ejemplos de aplicación del Método Simplex

Ejemplo para formular las ecuaciones con sus debidas restricciones:

Ejemplo: La empresa “Kekos” se dedica a la producción de 3 tipos de lámparas: de escritorio, manuales y colgantes. Para su uso se destinan 3 materias primas básicas denominadas A, B y C de las cuales su uso por día para cada lámpara y la disponibilidad máxima diaria se encuentra en la siguiente tabla:

La utilidad ($) que obtiene diariamente es 

• Lámparas de escritorio $1000.00 
• Lámparas manuales $500.00 
• Lámparas colgantes $2500.00 

Para formular el modelo el primer paso será identificar las variables y asignarles nombres, en este caso: 

• 𝑋1 = 𝐿á𝑚𝑝𝑎𝑟𝑎𝑠 𝑑𝑒 𝑒𝑠𝑐𝑟𝑖𝑡𝑜𝑟𝑖𝑜 
• 𝑋2 = 𝐿á𝑚𝑝𝑎𝑟𝑎𝑠 𝑚𝑎𝑛𝑢𝑎𝑙𝑒𝑠 
• 𝑋3 = 𝐿á𝑚𝑝𝑎𝑟𝑎𝑠 𝑐𝑜𝑙𝑔𝑎𝑛𝑡𝑒𝑠 

Una vez que se tiene el primer paso se puede plantear la función objetivo, en este caso lo que se pretende es maximizar la ganancia (utilidad) por la venta de cada producto (como los datos de ganancia son diarios, así como el uso de materia prima no es necesario hacer ninguna conversión dejando los datos tal y como se presentan), por lo tanto la ecuación resultante es: 

• 𝑀𝑎𝑥 𝑍 = 1000𝑋1 + 500𝑋2 + 2500𝑋3

Las restricciones del modelo hacen referencia a la disponibilidad máxima que tenemos de cada una de las materias primas que se emplean en el proceso, de esta forma se obtiene:

• 100𝑋1 + 80𝑋2 ≤ 200 

Es decir, la materia prima A sólo se emplea para la fabricación de lámparas de escritorio y manuales en ciertas cantidades (100 y 80 respectivamente), su uso no puede ser mayor a las 200 piezas diarias (≤). Este procedimiento se hace con cuantas limitaciones se tenga, entonces: 

• 90𝑋1 + 50𝑋2 + 100𝑋3 ≤ 250 
• 30𝑋1 + 100𝑋2 + 40𝑋3 ≤ 180 

Existe una restricción más llamada “de no negatividad” en la que nos indica que no se pueden producir cantidades negativas del bien X ¡no fabricamos menos 10 tazas o menos 5 lápices! 

• 𝑋1 ,𝑋2, 𝑋3 ≥ 0 

Juntando la función objetivo y las restricciones el modelo queda conformado de la siguiente manera (s.a. significará que la función objetivo estará sujeta a: 

• 𝑀𝑎𝑥 𝑍 = 1000𝑋1 + 500𝑋2 + 2500𝑋3
• 100𝑋1 + 80𝑋2 ≤ 200 
• 90𝑋1 + 50𝑋2 + 100𝑋3 ≤ 250 
• 30𝑋1 + 100𝑋2 + 40𝑋3 ≤ 180 
• 𝑋1 ,𝑋2, 𝑋3 ≥ 0

Con este procedimiento se puede obtener la primera parte de todo método simplex que es formular las ecuaciones con sus restricciones.

Ejemplo Paso a Paso del Método Simplex:

La empresa el SAMÁN Ltda. Dedicada a la fabricación de muebles, ha ampliado su producción en dos líneas más. Por lo tanto actualmente fabrica mesas, sillas, camas y bibliotecas. Cada mesa requiere de 2 piezas rectangulares de 8 pines, y 2 piezas cuadradas de 4 pines. Cada silla requiere de 1 pieza rectangular de 8 pines y 2 piezas cuadradas de 4 pines, cada cama requiere de 1 pieza rectangular de 8 pines, 1 cuadrada de 4 pines y 2 bases trapezoidales de 2 pines y finalmente cada biblioteca requiere de 2 piezas rectangulares de 8 pines, 2 bases trapezoidales de 2 pines y 4 piezas rectangulares de 2 pines. Cada mesa cuesta producirla $10000 y se vende en $ 30000, cada silla cuesta producirla $ 8000 y se vende en $ 28000, cada cama cuesta producirla $ 20000 y se vende en $ 40000, cada biblioteca cuesta producirla $ 40000 y se vende en $ 60000. El objetivo de la fábrica es maximizar las utilidades.

 

Paso 1: Modelación mediante programación lineal

Variables:

X1 = Cantidad de mesas a producir (unidades)

X2 = Cantidad de sillas a producir (unidades)

X3 = Cantidad de camas a producir (unidades)

X4 = Cantidad de bibliotecas a producir (unidades)

Restricciones:

2X1 + 1X2 + 1X3 + 2X4 <= 24

2X1 + 2X2 + 1X3 <= 20

2X3 + 2X4 <= 20

4X4 <= 16

Función Objetivo:

ZMAX = 20000X1 + 20000X2 + 20000X3 + 20000X4

Paso 2: Convertir las inecuaciones en ecuaciones

En este paso el objetivo es asignar a cada recurso una variable de Holgura, dado que todas las restricciones son «<=».

2X1 + 1X2 + 1X3 + 2X4 + 1S1 + 0S2 + 0S3 + 0S4 = 24

2X1 + 2X2 + 1X3 + 0X4 + 0S1 + 1S2 + 0S3 + 0S4 = 20

0X1 + 0X2 + 2X3 + 2X4 + 0S1 + 0S2 + 1S3 + 0S4 = 20

0X1 + 0X2 + 0X3 + 4X4 + 0S1 + 0S2 + 0S3 + 1S4 = 16

De esta manera podemos apreciar una matriz identidad (n = 4), formado por las variables de holgura las cuales solo tienen coeficiente 1 en su respectivo recurso, por el ejemplo la variable de holgura «S1» solo tiene coeficiente 1 en la restricción correspondiente a el recurso 1.

La función objetivo no sufre variaciones:

ZMAX = 20000X1 + 20000X2 + 20000X3 + 20000X4

Paso 3: Definir la solución básica inicial

El Método Simplex parte de una solución básica inicial para realizar todas sus iteraciones, esta solución básica inicial se forma con las variables de coeficiente diferente de cero (0) en la matriz identidad.

1S1 = 24

1S2  = 20

1S3 = 20

1S4  = 16

Solución: (segundo término)= En esta fila se consigna el segundo término de la solución, es decir las variables, lo más adecuado es que estas se consignen de manera ordenada, tal cual como se escribieron en la definición de restricciones.

Cj = La fila «Cj» hace referencia al coeficiente que tiene cada una de las variables de la fila «solución» en la función objetivo.

Variable Solución = En esta columna se consigna la solución básica inicial, y a partir de esta en cada iteración se van incluyendo las variables que formarán parte de la solución final.

Cb = En esta fila se consigna el valor que tiene la variable que se encuentra a su erecha «Variable solución» en la función objetivo.

Zj = En esta fila se consigna la contribución total, es decir la suma de los productos entre término y Cb.

Cj – Zj =  En esta fila se realiza la diferencia entre la fila Cj y la fila Zj, su significado es un «Shadow price», es decir, la utilidad que se deja de recibir por cada unidad de la variable correspondiente que no forme parte de la solución.

Solución inicial:

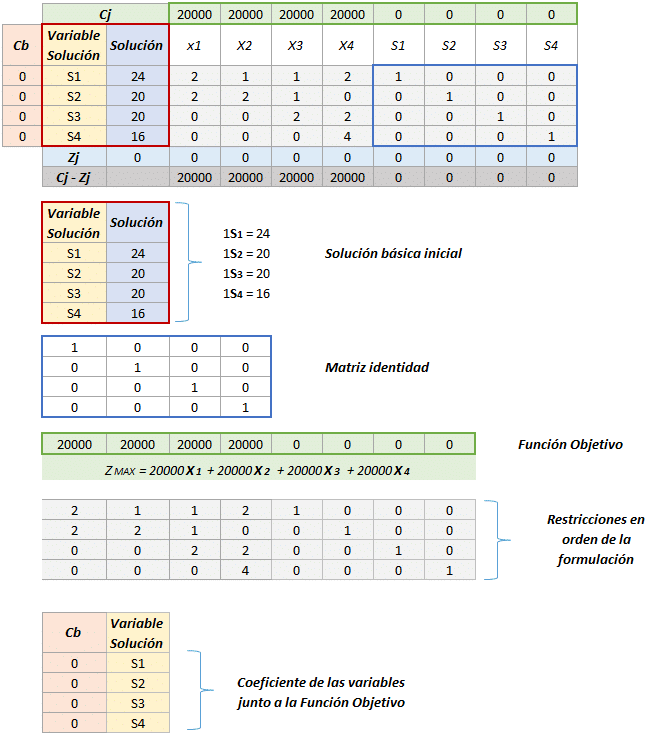
Paso 5: Realizar las iteraciones necesarias

Este es el paso definitivo en la resolución por medio del Método Simplex, consiste en realizar intentos mientras el modelo va de un vértice del poliedro objetivo a otro.

El procedimiento a seguir es el siguiente:

1. Evaluar que variable entrará y cual saldrá de la solución óptima:

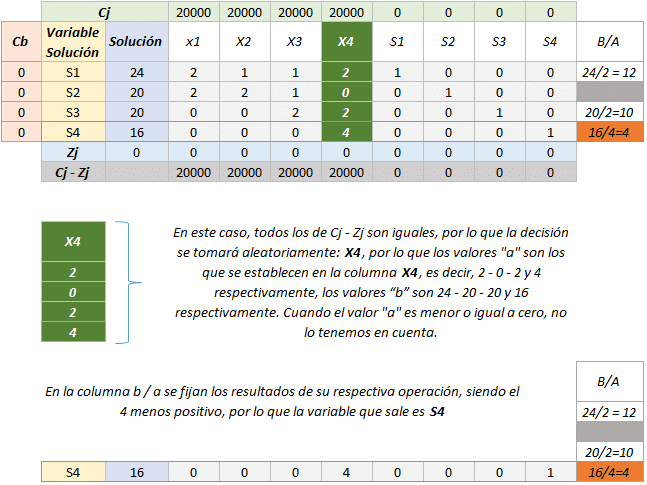
2. El hecho de que una variable distinta forme parte de las variables solución implica una serie de cambios en el tabulado Simplex, cambios que se explicarán a continuación.

• Lo primero es no olvidar el valor del «a» correspondiente a la variables a entrar, en este caso el «a = 4».

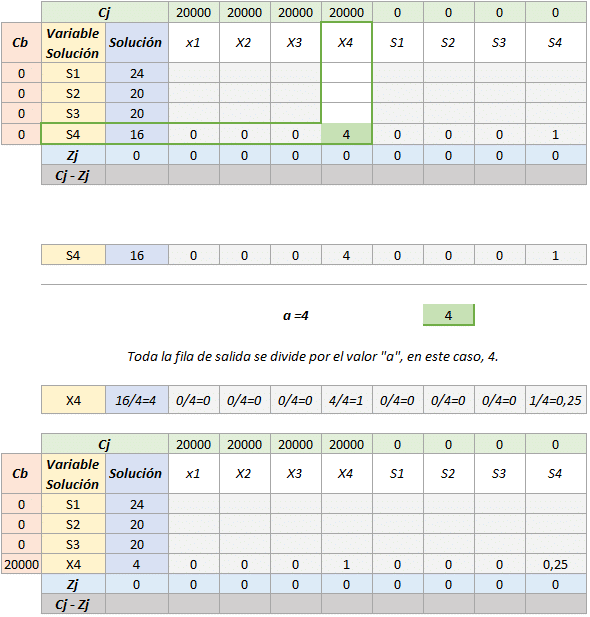
• Lo siguiente es comenzar a rellenar el resto de la tabla, fila x fila.

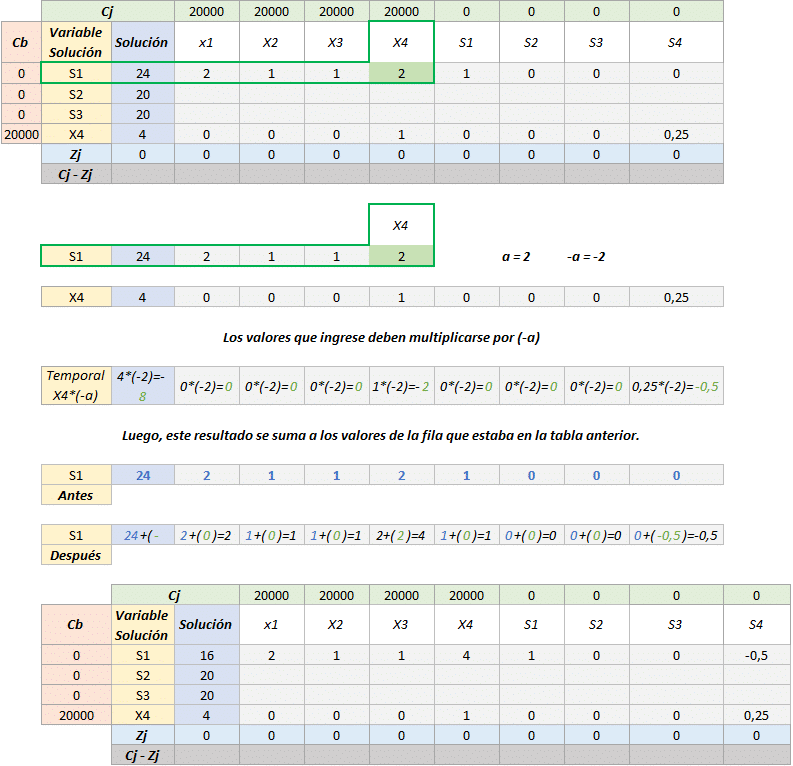
• Se repite este procedimiento con las dos filas restantes, ahora se harán los cálculos correspondientes en el resto de las celdas.

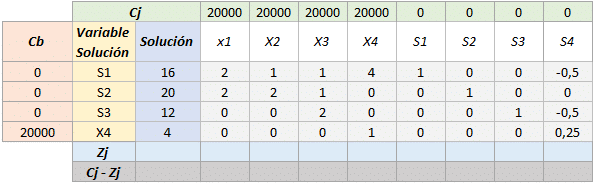
Una vez establecidos los valores de la matriz, puede calcular hasta llenar la tabla correspondiente a la primera iteración.

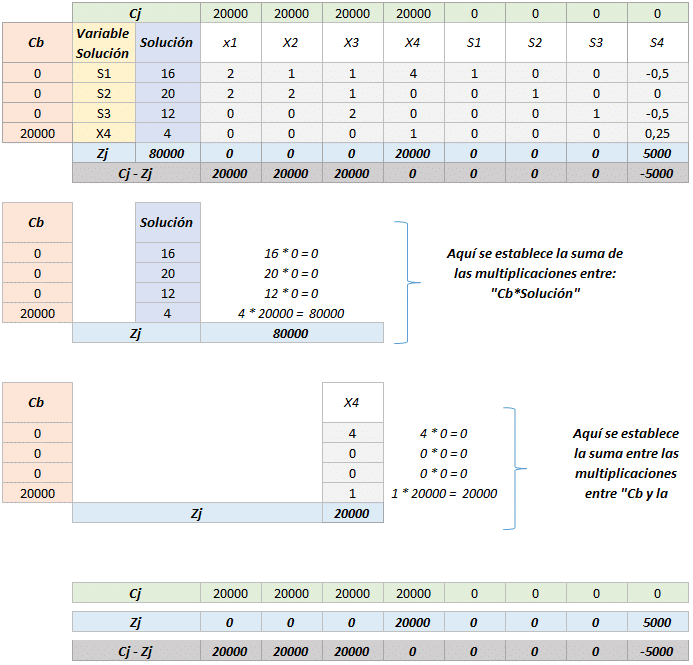
De esta manera se culmina la primera iteración, este paso se repetirá cuantas veces sea necesario y solo se dará por terminado el método según los siguientes criterios.

	Maximizar	Minimizar
Solución Óptima	Cuando todos los Cj – Zj sean <= 0	Cuando todos los Cj – Zj sean >= 0

• Continuamos con las iteraciones para lo cual tenemos que repetir los pasos anteriores.

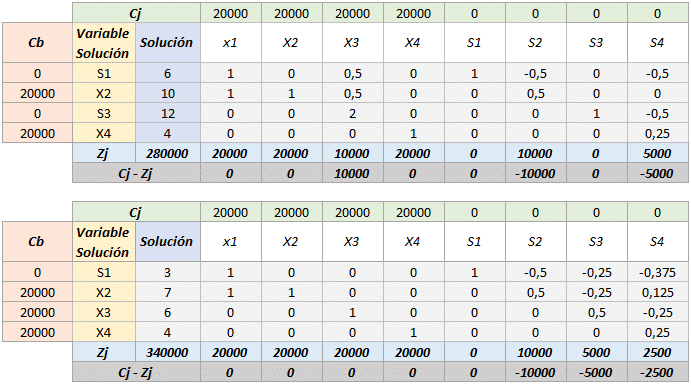
En esta última iteración podemos observar que se cumple con la consigna Cj – Zj <= 0, para ejercicios cuya función objetivo sea «Maximizar», por ende hemos llegado a la respuesta óptima.

X1 = 3

X2 = 4

X3 = 6

X4 = 4

Con una utilidad de: $ 340000

Sin embargo una vez finalizado el Método Simplex se debe observar una matriz identidad en el rectángulo determinado por las variables de decisión, el hecho de que en este caso no se muestre la matriz identidad significa que existe una solución óptima alterna.

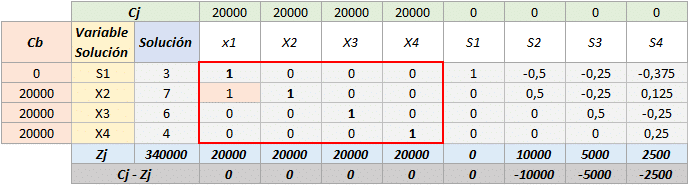
La manera de llegar a la otra solución consiste en alterar el orden en que cada una de las variables entró a la solución básica, recordemos que el proceso fue decidido al azar debido a la igualdad en el Cj – Zj del tabulado inicial. Aquí les presentamos una de las maneras de llegar a la otra solución.

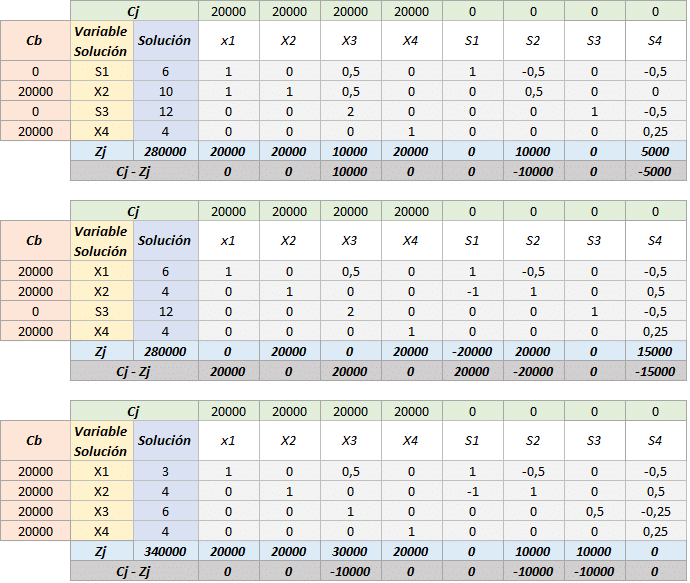
Podemos observar como existe una solución óptima alternativa en la cual la combinación de variables es distinta y existe un menor consumo de recursos, dado que el hecho de que se encuentre la variable «S1» en la solución óptima con un coeficiente de «3» significa que se presenta una holgura de 3 unidades del recurso (pieza rectangular de 8 pines).

X1 = 0 (Cantidad de mesas a producir = 0)

X2 = 7 (Cantidad de sillas a producir = 7)

X3 = 6 (Cantidad de camas a producir = 6)

X4 = 4 (Cantidad de bibliotecas a producir = 4)

S1 = 3 (Cantidad de piezas rectangulares de 8 pines sin utilizar =3)

Con una utilidad de: $ 340000

---

Problemas de minimización con el Método Simplex

Para resolver problemas de minimización mediante el algoritmo simplex existen dos procedimientos que se emplean con regularidad.

• El primero, que a mi juicio es el más recomendable se basa en un artificio aplicable al algoritmo fundamentado en la lógica matemática que dicta que «para cualquier función f(x), todo punto que minimice a f(x) maximizará también a – f(x)». Por lo tanto el procedimiento a aplicar es multiplicar por el factor negativo (-1) a toda la función objetivo.

A continuación se resuelve el algoritmo como un problema de maximización.

• El segundo procedimiento, el cual pretende conservar la minimización consiste en aplicar los criterios de decisión que hemos esbozado con anterioridad, en los casos de la variable que entra, que sale y el caso en el que la solución óptima es encontrada. Aquí recordamos los procedimientos según el criterio dado el caso «minimizar».